Exposant de Hurst et analyse financière

Dans la catégorie des indicateurs statistiques, on retrouve l’exposant de Hurst. D’abord utilisé dans l’hydrologie, cette méthode de calcul visait essentiellement à mesurer les occurrences de crues exceptionnelles. Par la suite, cet indicateur a été repris et popularisé par le mathématicien Benoît Mandelbrot (1924-2010). A l’origine de la compréhension des fractales, Benoît Mandelbrot est encore aujourd’hui un des plus grands chercheurs dans le domaine économique et financier. Pour rappel, les fractales consistent en la répétition de schémas de variation des prix sur différentes échelles de temps. Décryptage de l’exposant de Hurst.

L’exposant de Hurst

L’exposant de Hurst, ou coefficient de Hurst, tire son origine de l’hydrologie. A l’origine, Harold Edwin Hurst (1880-1978) a cherché à mesurer les fluctuations du niveau du Nil en Egypte. Le calcul développé par Hurst visait à mesurer la « dépendance de long terme », c’est-à-dire à quel point les fluctuations de court terme sont en capacité de décrire les fluctuations à long terme, ou non. L’intérêt des travaux de Hurst est donc de mesurer « la mémoire longue » d’une variable.

« De façon beaucoup plus générale, Hurst a montré que les lois suivantes s’appliquent à quantité de chroniques relatives à la météorologie : chutes d’eau, températures, pressions, etc… […] La découverte de Hurst possède donc un intérêt théorique aussi bien que pratique. On en conclut habituellement que les séries météorologiques ne sont pas stationnaires, même en première approximation […]. » – Fractales, hasard et finance (1997), Benoît Mandelbrot, page 26.

Dans la finance des ingénieurs, l’exposant de Hurst demeure utilisé. L’application de cette méthode n’est pourtant pas courante et reste cantonnée à quelques rares analystes. Pour aller plus loin.

Interprétation du coefficient de Hurst

Il advient ainsi trois interprétations suivant les différents valeurs du coefficient de Hurst (H) :

• 0 < H < 0,5… Si la valeur de H est comprise entre 0 et 0,5 alors l’actif aura tendance à connaître des variations successives entre hauts et bas. Ainsi, un plus bas à court terme laissera présager un plus haut dans le futur, et inversement. En outre, la fiabilité du signal augmente lorsque H se rapproche de 0. Aussi, une valeur de H inférieure à 0,33 est parfois considérée par certains analystes comme un signal puissant de retournement de tendance.
• H = 0,5… Si la valeur de H est de 0,5 alors il n’existe pas d’autocorrélation du cours de l’actif. C’est-à-dire que les retournements à court terme ne présagent en rien les retournements probables à venir dans le futur. Dans ce cas, le caractère fractal du cours est faible et l’indicateur ne nous permet pas de projeter une évolution future suffisante.
• 0,5 > H > 1… Si la valeur de H est comprise entre 0,5 et 1 alors un nouveau sommet à court terme aura tendance à traduire un nouveau sommet à long terme dans le futur. On parle aussi techniquement d’autocorrélation positive. En outre, la fiabilité du signal augmente lorsque H se rapproche de 1. Une valeur de H supérieure à 0,66 est aussi parfois considérée comme un signal puissant de persistance de tendance.

Remarque

Enfin, une remarque important est nécessaire. La valeur du coefficient de Hurst (H) n’est pas la même selon la période considérée. La valeur de H est généralement inférieure à 0,5 lorsqu’on mesure le coefficient sur des périodes de court terme (journalières ou inférieures). En conséquence, la valeur de H est aussi généralement supérieure à 0,5 et de plus en plus proche de 1 lorsque la période considérée est plus longue (hebdomadaire, mensuel, annuel…). La principale explication à ce phénomène réside dans une propriété de l’étude cyclique des marchés.

Utilisation du coefficient de Hurst en finance

Pour concrétiser l’application de ce coefficient, nous avons choisi le cas du Bitcoin (BTC). Nous avons ainsi sélectionné le coefficient sur une échelle hebdomadaire et une échelle journalière.

Le cas du Bitcoin (BTC) dans l’analyse du coefficient de Hurst

Le graphique ci-dessous montre le cours du Bitcoin (en haut, échelle logarithme) et le coefficient de Hurst (bas). Le graphique est sélectionné en données hebdomadaires. Les signaux de retournement suggérés par le coefficient de Hurst (H) sont représentés par des lignes verticales (orange). Le précédent signal de retournement baissier a été donné en avril 2021. Depuis, nous nous situons dans une tendance baissière qui est au stade de « tendance significative » actuellement (H > 0,66).

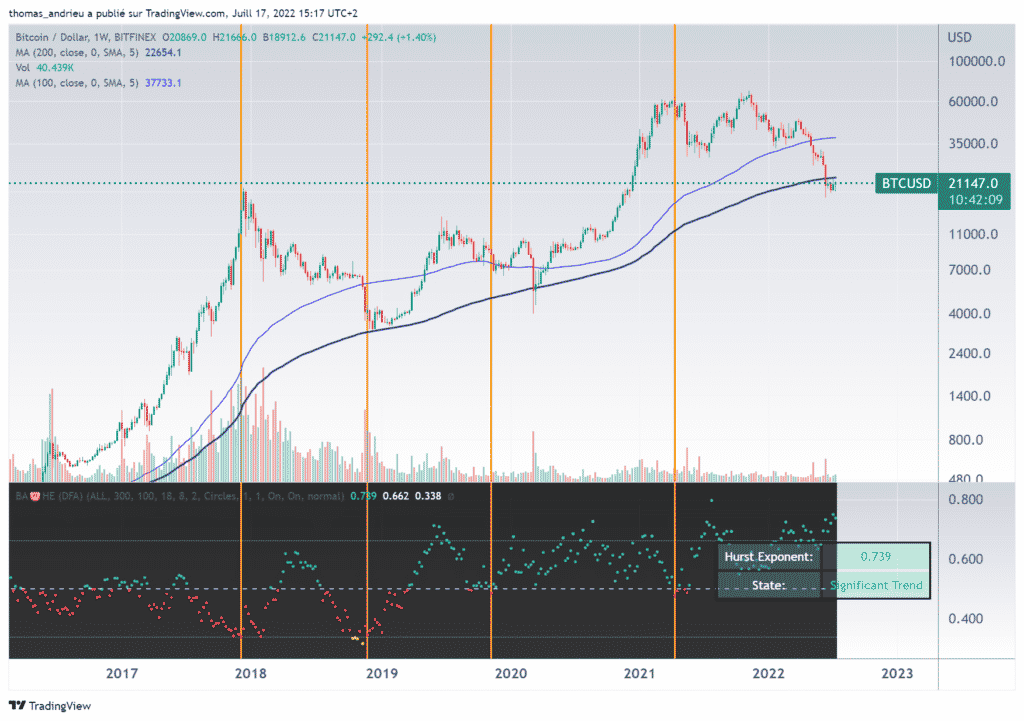
Il est important de noter qu’un coefficient H sous 0,5 ne signifie pas un retournement de long terme. Ce n’est que la validation d’un minimum de H qui impulse généralement un retournement. Ainsi, la tendance actuelle demeure fortement baissière et un retournement haussier long ne serait pas à attendre avant une chute du coefficient hebdomadaire sur les 0,5 au moins.

De plus, nous avons représenté le cours du Bitcoin et le coefficient de Hurst en journalier. Dans ce cas, la lecture des changements et retournements devient légèrement plus complexe. Le dernier signal de retournement suggéré le 7 mai par le coefficient de Hurst était baissier (après une évolution avec H > 0,5 ). La pleine tendance baissière a été atteinte le 19 juin d’après le coefficient, date du dernier plus bas majeur.

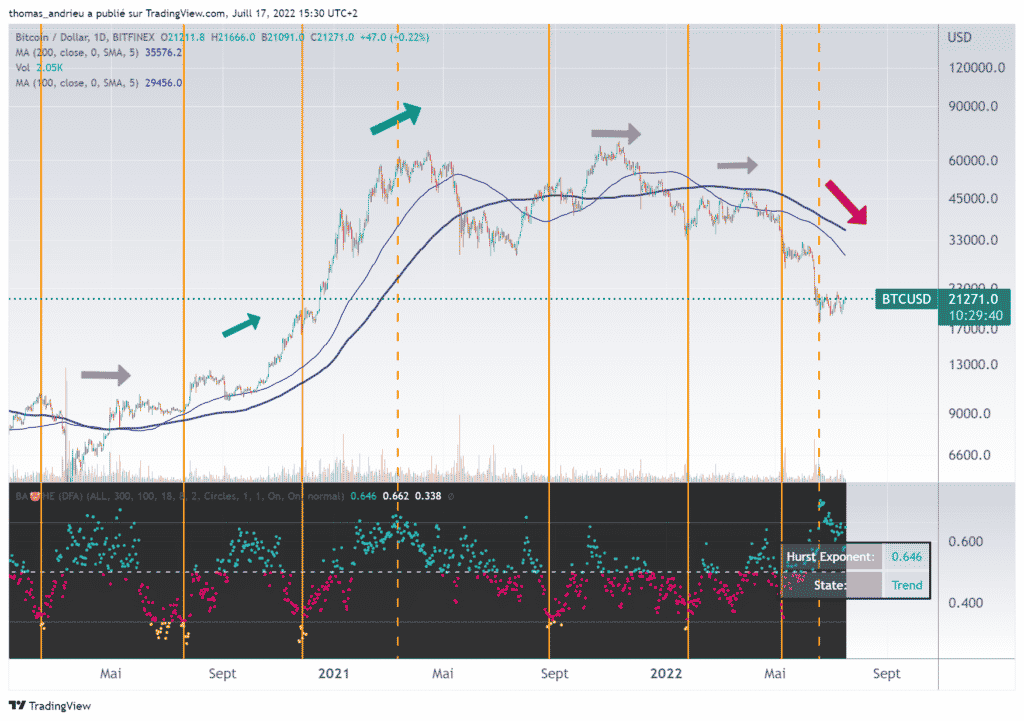
Ainsi, une évolution du coefficient entre 0 et 0,5 donnera souvent des signaux de retournement au sein d’une tendance neutre. A l’inverse, un signal de retournement (H < 0,33) suivi d’un rebond de H (H>0,5) indiquera un retournement suivi d’une forte tendance haussière ou baissière. Il faut avoir ici en tête que le coefficient de Hurst est un indicateur très pertinent pour les signaux puissants. Mais il est généralement nécessaire de le compléter par d’autres indicateurs par ailleurs.

Calcul du coefficient de Hurst…

Le calcul du coefficient de Hurst n’est pas forcément nécessaire dans la mesure où plusieurs plateformes proposent aujourd’hui un calcul du coefficient pour l’ensemble des valeurs désirées. Le coefficient de Hurst s’exprime par les termes suivants, que nous allons détailler :

H = R(n) / S(n)

On dit ainsi que H s’exprime comme le rapport (1)/(2) entre (1) la différence entre les écarts maximums et minimums à la moyenne des n séries précédentes et (2) l’écart type des n séries précédentes. Une valeur de H élevée traduit le fait qu’un actif connaît de grandes différences dans les écarts à la moyenne et/ou que sa volatilité est faible. En général, 5 étapes sont nécessaires au calcul de H :

1. Pour une série de N données, on divise en séries respectives de N/2, N/4… données. On calcule ensuite la moyenne des séries.
2. On établit ensuite une fonction qui mesure l’écart pour chaque série avec la moyenne observée. (Y = X – m, avec X la valeur de la série donnée et m la moyenne précédente).
3. On réalise la somme des écarts des n dernières séries (notons Z la somme des n derniers écarts Y).
4. La valeur R(n) dans le ratio s’obtient comme la différence entre la plus grande valeur de Z et la plus petite valeur de Z des n dernières séries. C’est la différence des plus grands écarts à la moyenne parmi les n dernières séries.
5. On calcule l’écart type (la volatilité) des n dernières séries (notons S(n) cette valeur).

Le ration est enfin obtenu comme le rapport entre R(n) et S(n).

Cycles et fractales

« La loi de Hurst est équivalente à la loi spectrale […]. En fait, à mesure que que T° augmente [longueur d’un échantillon de données], la tendance doit être réinterprétée comme manifestation d’un nombre toujours croissants de « cycles lents ». » – Fractales, hasard et finance (1997), Benoît Mandelbrot, page 28.

Benoît Mandelbrot, comme souligné dans ses différents travaux, s’est inspiré de l’étude des cycles pour comprendre la nature fractale des marchés. L’analyse des cycles de marché montre partout que les tendances longues sont le fait d’un nombre restreint de cycles longs. Les tendances courtes, qui paraissent plus irrégulières, sont en réalité la manifestation d’une multitude de cycles courts.

« La théorie des probabilités est basée sur le fait que des phénomènes aléatoires, considérés dans leur action collective à grande échelle, créent une régularité non-aléatoire » – Gnedenko & Kolmogorov, 1954.

Une inspiration majeure de Benoît Mandelbrot fut celle conférée par les travaux des mathématiciens Gnedenko & Kolmogorov. Les deux mathématiciens parlaient notamment de « régularité non aléatoire ». Ce terme est utilisé pour décrire le fait que la combinaison de phénomènes probabilistes pris individuellement génèrent des phénomènes « réguliers ». Lire plus à ce sujet : syndromeDeJoseph.pdf (yale.edu). Les fractales sont alors directement liées aux cycles. Les cycles sont une construction complexe, dans laquelle l’accumulation de fluctuations courtes influe directement sur la formation des cycles longs.

En conclusion

En bref, l’exposant de Hurst est un des indicateurs incontournables dans l’étude des fractales et des cycles de marché. Le coefficient de Hurst répondait originellement à la problématique de l’apparition de schémas d’évolution des prix différents (mais reliés) sur plusieurs échelles de temps. En d’autres termes, l’exposant de Hurst (H) mesure, si on peut toutefois le formuler ainsi, la « dispersion temporelle » d’un actif. Une valeur de H faible traduira une succession de plus hauts et de plus bas induits par le fait qu’une valeur de H inférieure à 0,5 présage un retournement dans le futur.

A l’inverse, une valeur de H élevée ( H > 0,5 ) sera généralement synonyme d’une tendance persistante. Un plus haut à court terme présagera un plus haut futur, et un plus bas à court terme présagera un plus bas futur. C’est la définition mathématique de la tendance boursière au sens de Dow !

Le coefficient de Hurst est donc un moyen d’anticiper la répétition de retournements présents dans le futur. Ce principe fractal, est aussi cyclique. A long terme, les tendances sont plus marquées (H est élevé) et les déviations de l’évolution historique de H sont généralement des signaux puissants. A court terme, les cycles baissiers sont plus récurrents, tout comme la volatilité, ce qui implique une valeur de H plus faible. Ici, le coefficient de Hurst nécessite plus d’indicateurs complémentaires et une étude plus approfondie de son évolution. En ce sens, l’étude des cycles ou des fractales est un moyen de relier les signaux de Hurst aux anticipations sur les marchés financiers.